CÁLCULO III - A RCN00067 – 2025-2
1 Informações Básicas
Início e Fim do Período: 18/08/2025 a 18/12/2025.
Horário e sala:
Quadro de Alocação de salas do IHS – acesso por celular
| Dia | Horário | Sala |
|---|---|---|
| Segunda | 14h - 16h | GP 17 |
| Terça | 16h - 18h | GP 17 |
Atendimento:
- Quartas 14h às 16h e Sextas 16h às 18h – Sala 104 do IHS (prédio alugado)
Material a ser utilizado
Ementa: Busque por RCN00075 em quadro de horários:
EQUAÇÕES PARAMÉTRICAS. FUNÇÕES VETORIAIS. SUPERFÍCIES QUÁDRICAS E CILÍNDRICAS. FUNÇÕES DE VÁRIAS VARIÁVEIS, LIMITE, CONTINUIDADE, DERIVADAS DIRECIONAIS, OTIMIZAÇÃO E MULTIPLICADORES DE LAGRANGE.
2 Apresentação do Curso
Este curso é constituído de dois módulos: Funções Vetoriais e Superfícies e Funções de Várias Variáveis.
O livro texto será referência [1], que está disponíveis para empréstimo na Biblioteca do campus – BRO. É altamente recomendado que vocês consultem este material, de preferência o livro físico.
As demais referência contidas na Seção 5 formam uma lista complementar/auxiliar do curso, foram usados principalmente na elaboração das notas de aulas e exemplos.
3 Avaliação
A avaliação será feita mediante 3 Verificações de Aprendizagem (VAs) Escritas. A média parial (NP) será a média aritmética entre elas, isto é, \[NP=\frac{VA_1+VA_2+VA_3}{3}\] De acordo com o Regulamento da UFF, a Nota Final é calculada da seguinte forma:
Definida como sendo igual à média parcial, caso o discente tenha obtido aprovação direta, ou igual a 6(seis), se a aprovação foi obtida na verificação suplementar (VS). No caso de reprovação na VS, a nota final será o resultado do cálculo da média aritmética entre a média parcial e a nota obtida na VS.
Objetivos
As VAs tem como objetivos avaliar se o aluno:
- É capaz de interpretar as questões corretamente e formular soluções para os problemas propostos.
- É capaz de produzir soluções, em formato de texto, compreensíveis, com nível de detalhamento e rigor adequados para que outros profissionais familiarizados com os conceitos possam entendê-las.
- Aprendeu os conceitos e técnicas ensinados em sala de aula.
- Sabe determinar quando a solução proposta resolve de fato o problema.
- Consegue desenvolver uma argumentação lógica-dedutiva para chegar-se à resposta final.
Critério de correção das VAs
Com base nos objetivos apresentados acima, os critério de correção serão:
- Interpretação correta das questões.
- As soluções devem ser escrita com clareza, organização, rigor e detalhamento.
- Soluções desenvolvidas fora do conteúdo ensinado, mesmo que corretas, não serão consideradas.
- Questão com várias soluções será anulada.
- Resposta correta com solução errada será anulada.
Além disso, durante às VAs, serão adotadas as seguinte medidas:
- Proibido compartilhar material.
- Só é permitida a saída após entrega definitiva da VA, ou seja, não é permitido ir ao banheiro ou beber água. A VA tem duração de no máximo 2 horas.
- É permitida a consulta a material (livros, notas de aula, caderno, apostilas e etc.) e uso de dispositivo computacional, como calculadora científica, ambos sem acesso a internet.
- Fraude detectada, mesmo depois, zera a nota.
Segunda Chamada
O Art. 98 do Regulamento dos Cursos de graduação garante ao aluno o direito a uma avaliação de Segunda Chamada (VR), sem a necessidade de justificativa! Portanto, aquele aluno que não puder ou não quiser fazer uma das VAs, poderá faltar que seu direito à Segunda Chamada será garantido.
O conteúdo da Segunda Chamada será toda a matéria do semestre.
Como não há a necessidade de justificar a falta nas avaliações para ter o direito à Segunda Chamada garantido, alguns alunos usam este direito para fazer a Segunda Chamada quando não se sentem suficientemente preparados para alguma das avaliações.
Por conta disso, o aluno que estiver em dúvida entre fazer a VA ou a Segunda chamada, poderá comparecer no dia da VA e tentar fazê-la. Caso não se sinta preparado, poderá desistir e ainda terá o direito a fazer a Segunda Chamada. Aqueles que permanecerem e entregarem definitivamente a VA não terão o direito à Segunda Chamada.
Verificação Suplementar
Em concordância com o Regulamento dos Cursos de graduação em seu Art. 99, a Verificação Suplementar (VS) é vetada aos discentes já aprovados e é obrigatória para aqueles que tenham obtido média parcial entre 4.0 e 5.9, sendo esses dois limites incluídos.
4 Listas de Exercícios
Abaixo seguem os execícios da referência [1] que devem ser feitos. A distribuição está dada por seção.
Veja a lista aqui
O símbolo ✏️ significa quais exercícios já podem ser feitos com o contéudo dado até o momento, enquanto o símbolo 🔒 se refere àqueles que ainda não. A medida que o conteúdo em sala for avançando, novos exercícios serão desbloqueados.
- Parametrização, coordenadas polares, superfícies e funções vetoriais
✏️ § 12.5 (Retas e Planos): 3, 5, 7, 9, 23, 26, 31, 43, 45.
✏️ § 12.6 (Cilindros e Quádricas): 3, 5, 13, 15, 21-28, 29, 31, 33.
✏️ § 10.3 (Coordenadas Polares): 1, 3, 7, 9, 11, 15, 17, 19, 21, 23, 25, 29, 31, 33, 35, 37, 39, 41, 56.
✏️ § 13.1 (Funções Vetoriais): 7, 9, 11, 19-24, 27, 37, 38, 39.
✏️ § 13.2 (Derivadas): 3, 5, 17, 19, 21, 23, 25, 27 e 29.
✏️ §13.3 (Comprimento de arco e Curvatura): 1, 3, 5, 11, 13, 15, 17(b), 19(b), 21, 23.
✏️ § 13.4 (Velociade e Aceleração): 3, 5, 11, 13, 19, 31,32, 41.
- Funções de Várias Variáveis
✏️ § 14.1 (Funções): 11, 13, 15, 17, 19, 23, 25, 27, 30, 39, 41, 45, 49, 61, 63.
✏️ § 14.2 (Limite e Continuidade): 5, 7, 9, 11, 13, 15, 29, 31, 35, 39, 41.
✏️ § 14.3 (Derivadas Parciais): 15, 17, 21, 23, 25, 29, 31, 39, 41, 51, 53, 61, 63, 65.
✏️ § 14.4 (Aproximação Linear): 1, 3, 5, 11, 13, 21, 25, 27, 33, 35, 37.
✏️ § 14.5 (Regra da Cadeia): 1, 3, 5, 7, 15, 17, 19, 21, 23, 35, 43.
✏️ § 14.6 (Vetor Gradiente): 5, 7, 9, 11, 15, 17, 21, 23, 25, 29, 31, 34, 39, 41, 53.
✏️ § 14.7 (Máximos e Mínimos): 5, 7, 13, 15, 31, 33, 34, 35, 39, 41, 43, 47, 53.
✏️ § 14.8 (Multiplicadores de Lagrange): 3, 5, 9, 15, 17, 19, 41, 43.
Exercícios do Stewart Vol. 2, 7ª Edição.
✏️ § 14.7: 5, 7, 11, 13, 15, 31, 33, 34, 35, 39, 41, 43, 47, 53.
✏️ § 14.8: 3, 5, 9, 15, 17, 19, ,21, 45.
5 Referências
6 Cronograma Efetivado
A seguir temos a proposta de cronograma para este curso. Esta proposta pode sofrer pequenas alterações ao longo do curso que, caso ocorram, serão comunicadas aos alunos. Cabe ressaltar que o semestre se encerra no dia 18/12 , neste caso, é aconselhado que fiquem disponíveis até esta data.
1. Funções vetoriais e Superfícies
01 . Seg – 18/08 – Apresentação do estudantes. Apresentação do curso. Motivação.
02 . Ter – 19/08 – Revisão de equação paramétrica da reta e equação cartesiana do plano em \(\mathbb{R}^3\). Coordenadas Polares.
03 . Seg – 25/08 – Cancelamento da aula – Reunião PG
04 . Ter – 26/08 – Coordenadas Polares (continuação) Superfícies Cilíndricas. Superfícies Quádricas.
05 . Seg – 01/09 – Funções Vetoriais. Limite e continuidade. Curvas parametrizadas no Plano. Curvas parametrizadas no Espaço. Hélices.
06 . Ter – 02/09 – Parametrização de curvas como interseção de duas superfícies. Derivadas e regras de derivação de funções vetoriais.
🏖️ Dom – 07/09 – Independência
07 . Seg – 08/09 – Comprimento de arco. Parametrização pelo comprimento de arco. Vetor Tangente
08 . Ter – 09/09 – Curvatura. Definição de Curvatura. Fórmulas da curvatura. Movimento, velocidade e aceleração.
09 . Seg – 15/09 – Aula de Exercícios
10 . Ter – 16/09 – Aula de Exercícios
❓ Sex – 19/09 – Atendimento: 1 aluno compareceu
11 . Seg – 22/09 – Aula de Exercícios
12 . Ter – 23/09 – VA 1 (Verificação de Aprendizagem) gabarito
❓ Qua – 24/09 – Atendimento: 0 alunos compareceram
2. Funções de Várias Variáveis
13 . Seg – 29/09 – Definição de Funções de Várias Variáveis. Gráficos de funções de 2 variáveis. Curvas de Nível. Superfícies de nível.
14 . Ter – 30/09 – Não houve aula.
15 . Seg – 06/10 – Limites e continuidade.
16 . Ter – 07/10 – Derivadas Parciais. Derivadas de ordem superior.
🏖️ Dom – 12/10 – Nossa Senhora Aparecida
17 . Seg – 13/10 – Função de classe \(C^1\). Regra da cadeia. Vetor Gradiente. Plano tangente.
18 . Ter – 14/10 – Derivadas direcionais. Propriedades do vetor Gradiente
🏖️ Qua – 15/10 – Dia do Professor
🏖️ Seg – 20/10 – Semana Nacional de Ciência e Tecnologia
🏖️ Ter – 21/10 – Semana Nacional de Ciência e Tecnologia
🏖️ Seg – 27/10 – Ponto Facultativo
🏖️ Ter – 28/10 – Servidor Público
🏖️ Dom – 02/11 – Finados
19 . Seg – 03/11 – Aula de Exercícios
20 . Ter – 04/11 – Aula de Exercícios
21 . Ter – 10/11 – VA 2(verificação de Aprendizagem) gabarito
22 . Ter – 11/11 – Valores Máximo e Mínimo. Pontos críticos. Teste da Derivada Segunda Topologia do \(\mathbb{R}^2\). Máximos e Mínimos absolutos. Teorema de Weiestrass.
🏖️ Sáb – 15/11 – Proclamação da República
23 . Seg – 17/11 – Multiplicadores de Lagrange em \(\mathbb{R}^2\). Multiplicadores de Lagrange em \(\mathbb{R}^3\)
24 . Ter – 18/11 – Aproximação linear. Diferenciais em \(\mathbb{R}^2\) e \(\mathbb{R}^3\).
🏖️ Qui – 20/11 – Consciência Negra
25 . Seg – 24/11 – vista da VA2.
26 . Ter – 25/11 – Aula de exercícios.
27 . Seg – 01/12 – Aula de Exercícios
28 . Ter – 02/12 – VA 3 (Verificação de Aprendizagem) gabarito
Provas Finais
29 . Seg – 08/12 – –
30 . Ter – 09/12 – VR gabarito
31 . Seg – 15/12 – VS
32 . Ter – 16/12 – –
🔚 Qui – 18/12 – Fim do Período. 🙌
Dados do Semestre
número total de aulas necessárias incluíndo provas: 30
número total de semanas do semestre: 18
número de semanas sem os feriados: 16
dias letivos: 32
feriados: 10
feriado em dias de aulas: 4
7 Resultados
1ª Verificação
Compareceram à 1ª verificação 31 alunos, de um total de 33 inscritos, isto é, 93.94 %.
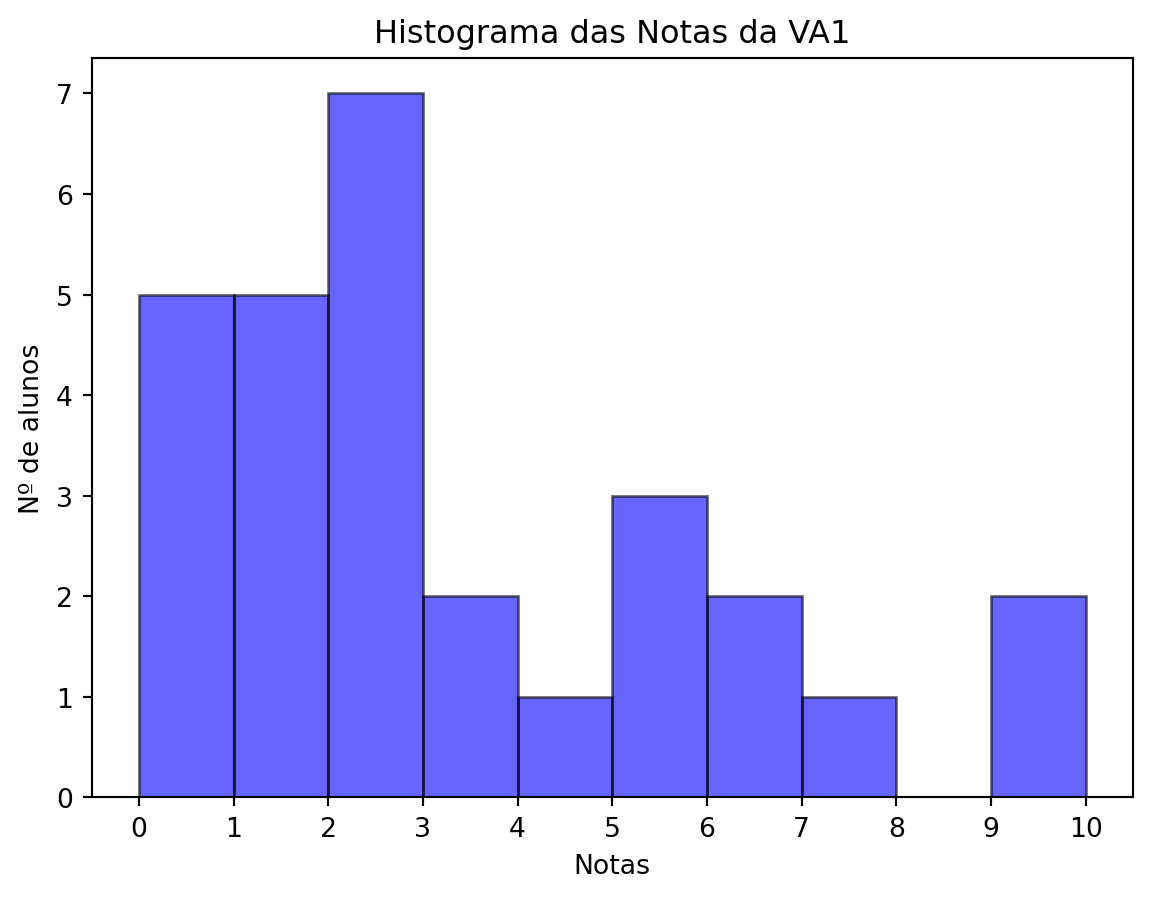
| Classificação | Nº alunos | Porcentagem |
|---|---|---|
| Notas acima de 6 | 10 | 32.26 % |
| Notas entre 4 e 6 | 5 | 16.13 % |
| Notas abaixo de 4 | 16 | 51.61 % |
| Total | 31 | 100 % |
=== Medidas de Tendência Central ===
Média: 4.35
Mediana: 3.10
Média Aparada (10%): 4.24
=== Forma da Distribuição ===
Assimetria: 0.37
Curtose: -1.15
2ª Verificação
Compareceram à 2ª verificação 32 alunos, de um total de 33 inscritos, isto é, 96.97 %.
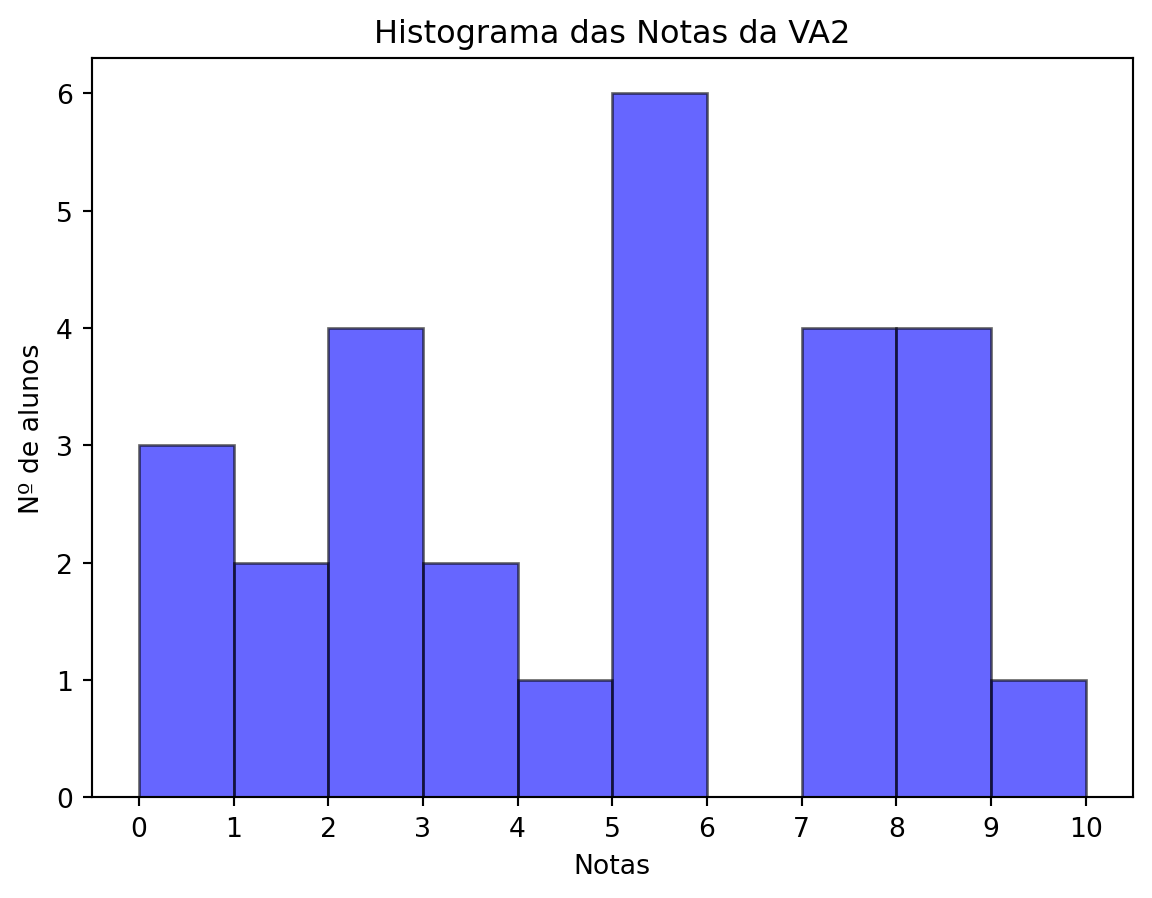
| Classificação | Nº alunos | Porcentagem |
|---|---|---|
| Notas acima de 6 | 9 | 28.12 % |
| Notas entre 4 e 6 | 11 | 34.38 % |
| Notas abaixo de 4 | 12 | 37.5 % |
| Total | 32 | 100 % |
=== Medidas de Tendência Central ===
Média: 4.73
Mediana: 5.25
Média Aparada (10%): 4.72
=== Forma da Distribuição ===
Assimetria: -0.01
Curtose: -1.12
3ª Verificação
Compareceram à 3ª verificação 29 alunos, de um total de 33 inscritos, isto é, 87.88 %.
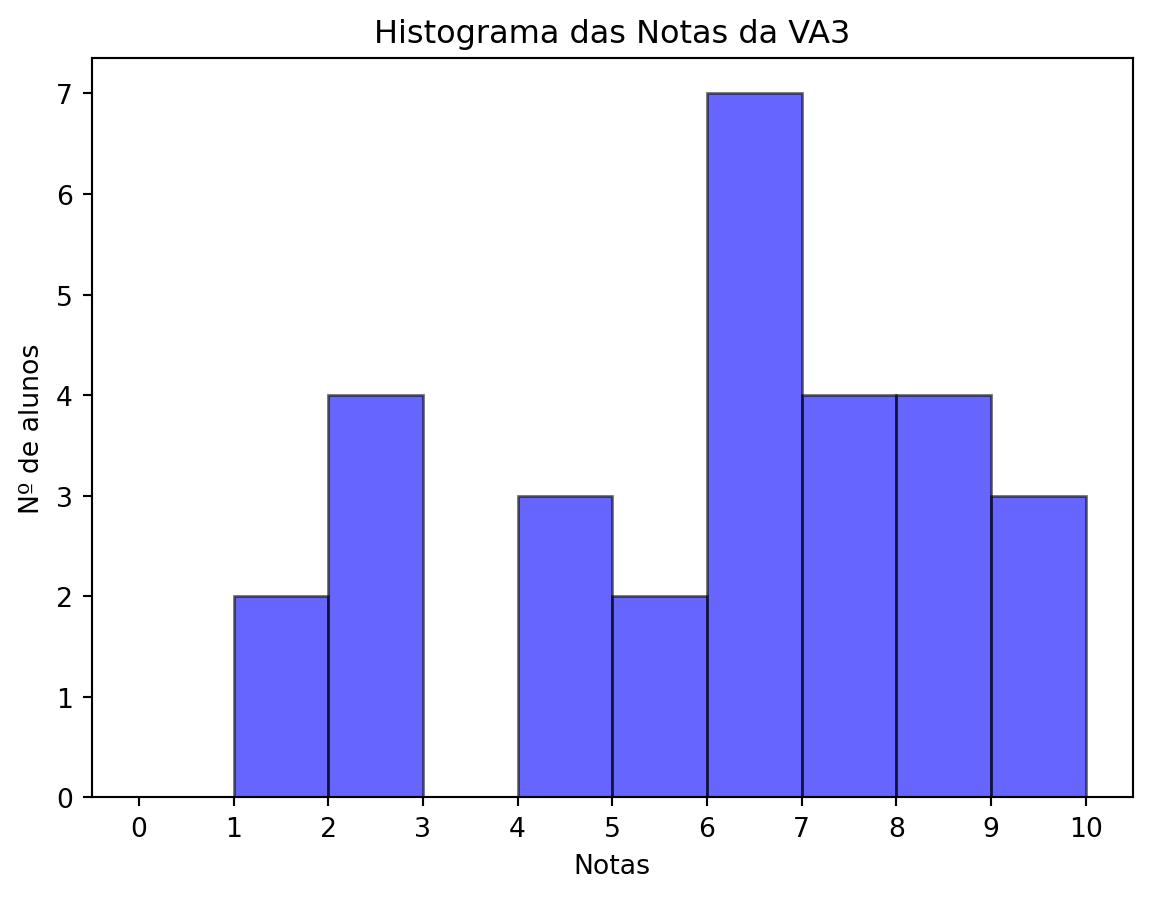
| Classificação | Nº alunos | Porcentagem |
|---|---|---|
| Notas acima de 6 | 18 | 62.07 % |
| Notas entre 4 e 6 | 5 | 17.24 % |
| Notas abaixo de 4 | 6 | 20.69 % |
| Total | 29 | 100 % |
=== Medidas de Tendência Central ===
Média: 5.88
Mediana: 6.50
Média Aparada (10%): 5.98
=== Forma da Distribuição ===
Assimetria: -0.52
Curtose: -0.72
Reusultados Finais
| Aprovados | 7 | 21.21 % |
| Reprovados | 16 | 48.48 % |
| VS | 10 | 30.3 % |
| Total | 33 | 100 % |
| Aprovados | 7 | 21.21 % |
| Reprovados | 26 | 78.79 % |
| Total | 33 | 100 % |
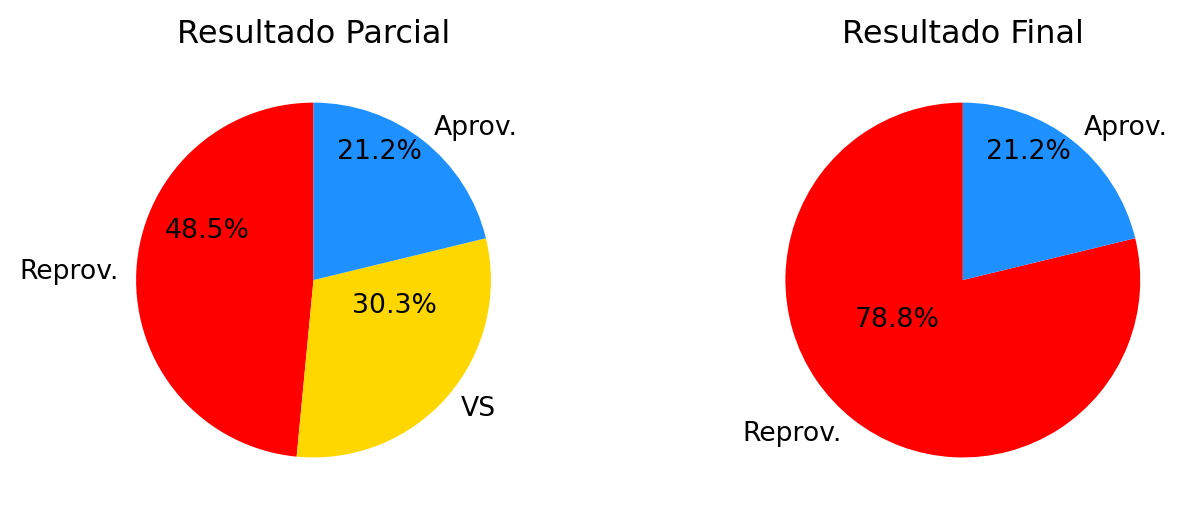
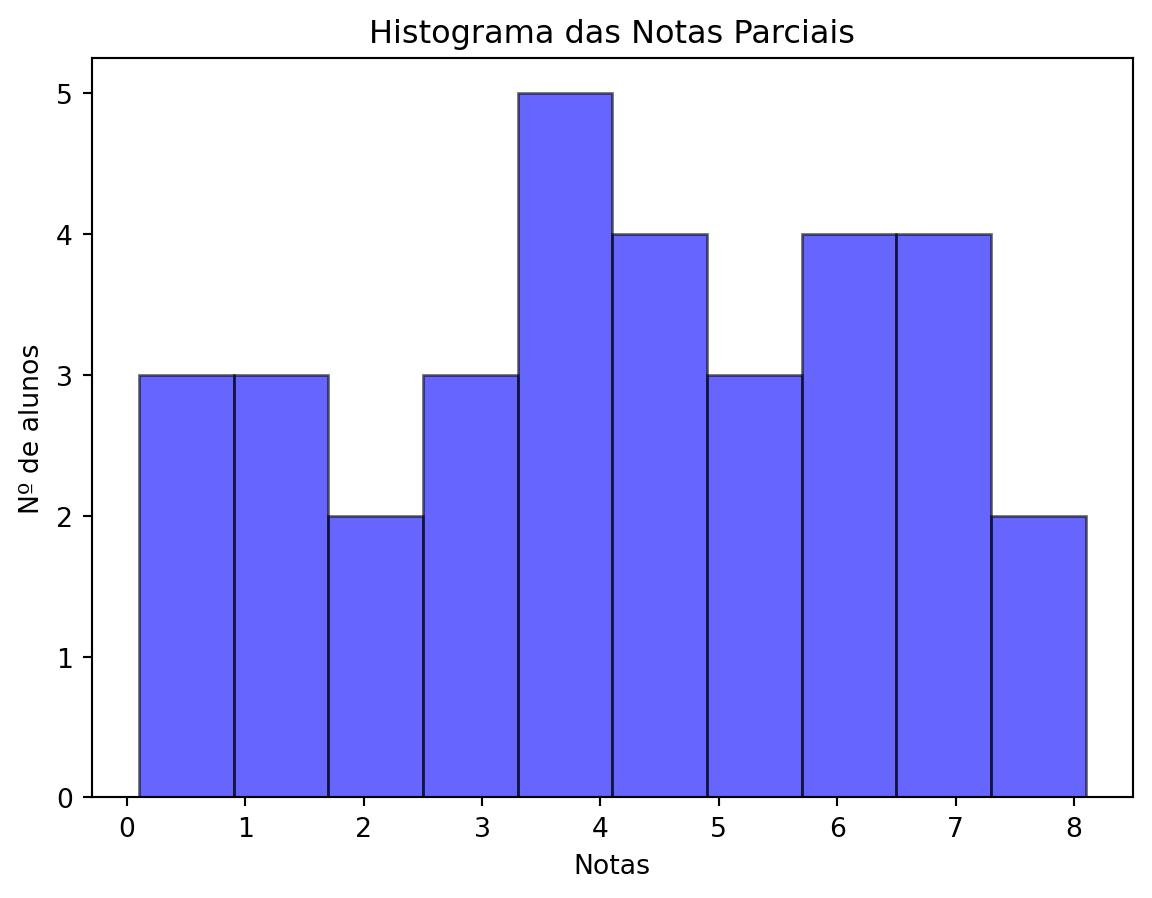
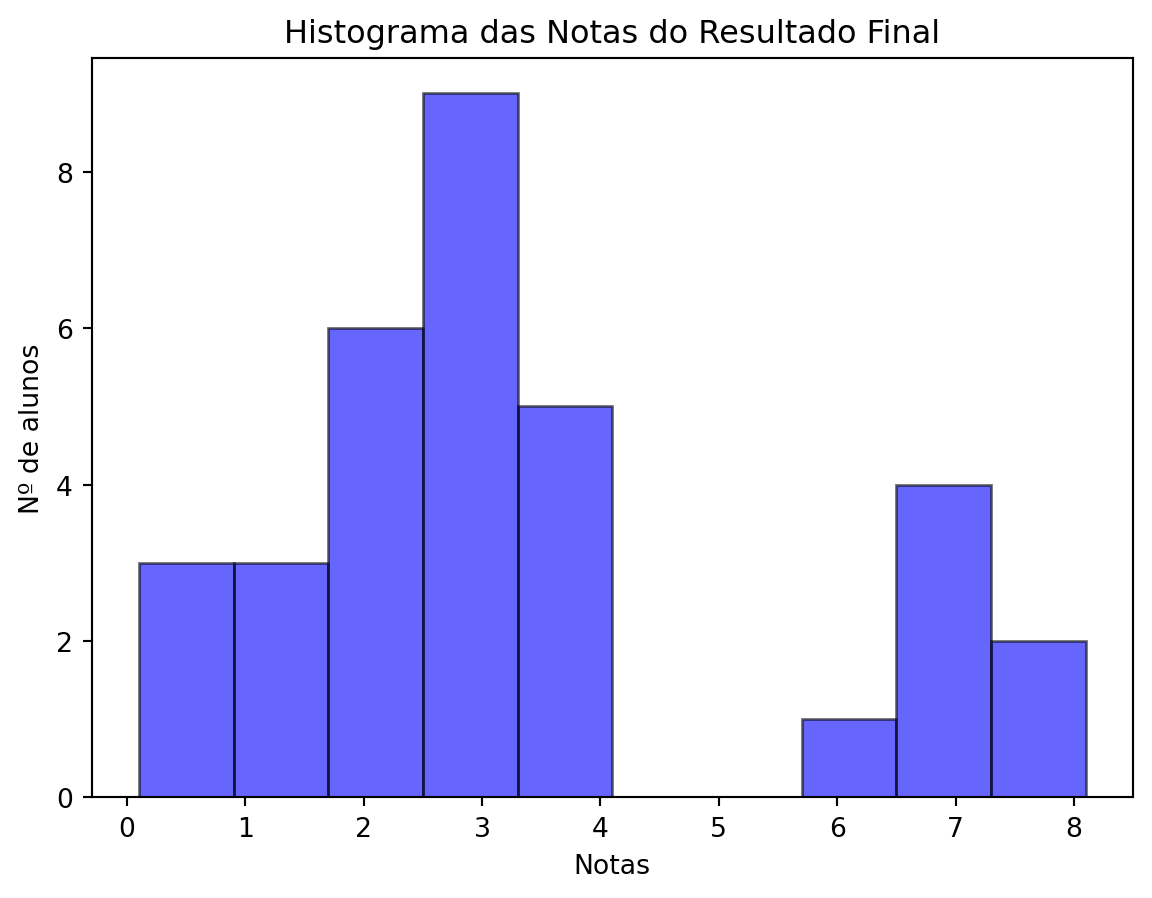
=== Medidas de Tendência Central ===
Média: 3.38
Mediana: 2.90
Média Aparada (10%): 3.24
=== Forma da Distribuição ===
Assimetria: 0.79
Curtose: -0.30
Resultados: concluintes
Cálculo III - 2025-1
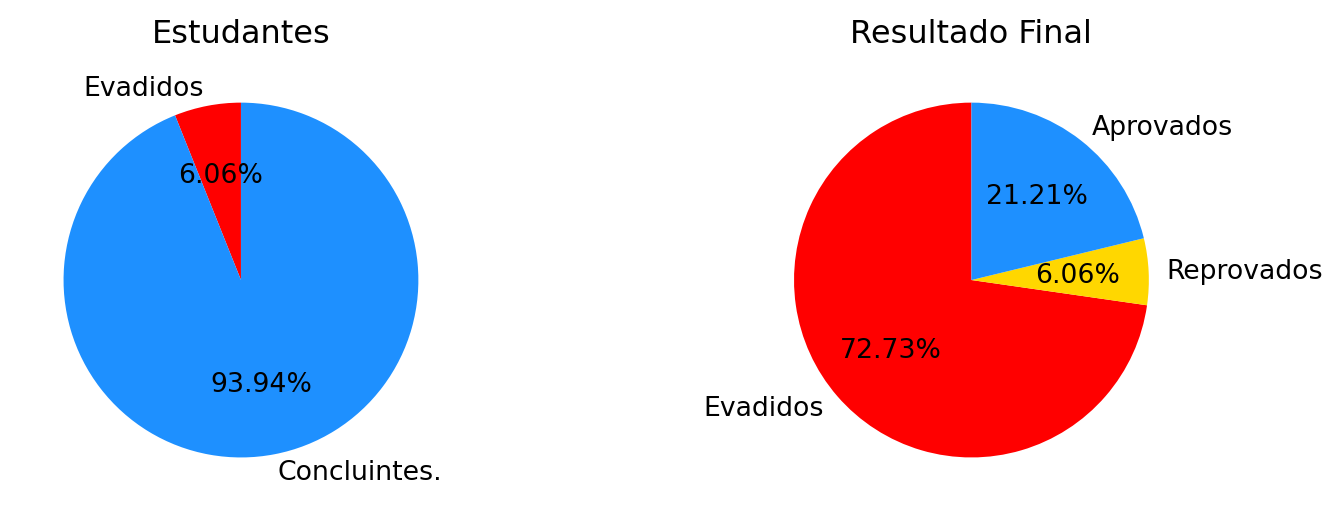
Tivemos 33 inscritos e uma evasão de 2 ( 6.06 %) estudantes, isto é, não realizaram nenhuma avaliação. Assim 31 ( 93.94 %) efetivamente concluíram a disciplina.
| Aprovados | 7 | 21.21 % |
| Reprovados | 24 | 72.73 % |
| Evadidos | 2 | 6.06 % |
| Total | 33 | 100 % |
8 Cronograma Proposto Inicialmente
Este foi o programa proposto no início do perído, que será mantido aqui para fins de comparação com o cronograma que realmente foi efetivado acima.
1. Funções vetoriais e Superfícies
01 . Seg – 18/08 – Apresentação do estudantes. Apresentação do curso. Motivação: problemas de otimização.
02 . Ter – 19/08 – Revisão de equação paramétrica da reta e equação cartesiana do plano em \(\mathbb{R}^3\). Coordenadas Polares.
03 . Seg – 25/08 – Superfícies Cilíndricas. Superfícies Quádricas.
04 . Ter – 26/08 – Aula de Exercícios 1
05 . Seg – 01/09 – Funções Vetoriais. Limite e continuidade. Curvas parametrizadas no Plano.
06 . Ter – 02/09 – Curvas parametrizadas no Espaço. Hélices. Parametrização de curvas como interseção de duas superfícies.
🏖️ Dom – 07/09 – Independência
07 . Seg – 08/09 – Derivadas e regras de derivação de funções vetoriais. Comprimento de arco.
08 . Ter – 09/09 – Parametrização pelo comprimento de arco. Vetor Tangente e Curvatura.
09 . Seg – 15/09 – Definição de Curvatura. Fórmulas da curvatura.
10 . Ter – 16/09 – Movimento, velocidade e aceleração.
11 . Seg – 22/09 – Aula de Exercícios 2
12 . Ter – 23/09 – VA 1 (Verificação de Aprendizagem)
2. Funções de Várias Variáveis
13 . Seg – 29/09 – Definição de Funções de Várias Variáveis. Gráficos de funções de 2 variáveis. Curvas de Nível. Superfícies de nível.
14 . Ter – 30/09 – Limites e continuidade.
15 . Seg – 06/10 – Derivadas Parciais. Derivadas de ordem superior. EPDs: Funções Harmônicas e Equação da Onda.
16 . Ter – 07/10 – Função de classe \(C^1\). Regra da cadeia.
🏖️ Dom – 12/10 – Nossa Senhora Aparecida
17 . Seg – 13/10 – Vetor Gradiente. Derivadas direcionais. Propriedades do vetor Gradiente
18 . Ter – 14/10 – Plano tangente. Aproximação linear.
🏖️ Qua – 15/10 – Dia do Professor
🏖️ Seg – 20/10 – Semana Nacional de Ciência e Tecnologia
🏖️ Ter – 21/10 – Semana Nacional de Ciência e Tecnologia
🏖️ Seg – 27/10 – Ponto Facultativo
🏖️ Ter – 28/10 – Servidor Público
🏖️ Dom – 02/11 – Finados
19 . Seg – 03/11 – Aula de Exercícios 3
20 . Ter – 04/11 – VA 2 (Verificação de Aprendizagem)
21 . Seg – 10/11 – Valores Máximo e Mínimo. Pontos críticos. Teste da Derivada Segunda
22 . Ter – 11/11 – Topologia do \(\mathbb{R}^2\). Máximos e Mínimos absolutos. Teorema de Weiestrass.
🏖️ Sáb – 15/11 – Proclamação da República
23 . Seg – 17/11 – Multiplicadores de Lagrange em \(\mathbb{R}^2\). Multiplicadores de Lagrange em \(\mathbb{R}^3\)
24 . Ter – 18/11 – Diferenciais em \(\mathbb{R}^2\) e \(\mathbb{R}^3\).
🏖️ Qui – 20/11 – Consciência Negra
25 . Seg – 24/11 – Derivação Implícita e Teorema da Função Implícita em \(\mathbb{R}^2\).
26 . Ter – 25/11 – Derivação Implícita e Teorema da Função Implícita em \(\mathbb{R}^3\).
27 . Seg – 01/12 – Aula de Exercícios 4
28 . Ter – 02/12 – VA 3 (Verificação de Aprendizagem)
Provas Finais
29 . Seg – 08/12 – VR
30 . Ter – 09/12 – —
31 . Seg – 15/12 – VS
32 . Ter – 16/12 – –
🔚 Qui – 18/12 – Fim do Período. 🙌